Symmetry is the balanced arrangement of atoms in a molecule. In Pharmaceutical Chemistry, a molecule’s elements of symmetry tells us if a drug is optically active or not. The binding of drug molecules to the target receptor in the body depends on symmetry of molecule. Thus, symmetry of any molecule affects optical activity and pharmacological potency.
Introduction: Why Symmetry Matters?
Before diving into the math, start with the “Why.”
- Definition: Elements of symmetry are geometric entities (points, lines, or planes) about which symmetry operation is performed. It is used to determine if a molecule is chiral or achiral. Think of Symmetry Elements as the “structural DNA”
- The Golden Rule: A molecule is chiral only if it lacks certain elements of symmetry (specifically Sn).
- Pharmacy Link: Mention how the symmetry of a molecule dictates its fit into a biological receptor (Lock and Key hypothesis).
Elements of Symmetry
Let’s break this down into four simple tools you can use to scan any molecule.
A. Plane of Symmetry (σ)
Also known as the “Mirror Plane.” It is an imaginary plane that bisects a molecule into two halves that are mirror images of each other. Imagine slicing an apple perfectly in half so that the left side is a mirror image of the right. That “slice” is the plane of symmetry.
- Key Concept: If a molecule has a σ plane, it is achiral or optically inactive (even if it has chiral centers, like meso compounds).
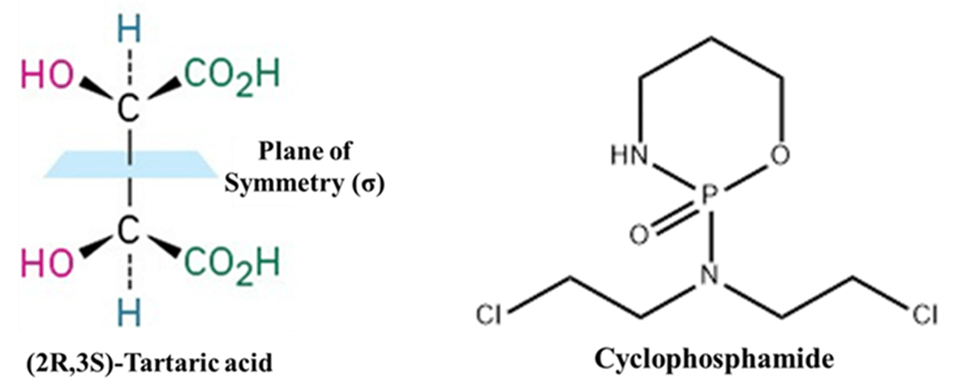
- Example: (2R,3S)–Tartaric acid (meso form). It has two chiral centers but is optically inactive because of the internal mirror plane (plane of symmetry).
- Cyclophosphamide: Cyclophosphamide is a well-known alkylating agent used in chemotherapy. While the phosphorus atom can be a chiral center, certain orientations or simplified analogs of the oxazaphosphorine ring possess a plane of symmetry. A plane passing through the phosphorus and nitrogen atoms bisects the ring. Because it has a plane of symmetry, the molecule (in that specific conformation) is achiral.
B. Center of Symmetry (i) – The “Dead Center”
Think of this as a point in the very middle of the molecule. In the molecule, each atom has identical atom opposite at equal distance. It is also called as the “Center of Inversion.” It is a point within a molecule such that any line drawn from an atom through that point encounters an identical atom at an equal distance on the opposite side.
- Key Concept: Common in cyclic structures and certain trans-isomers. If i is present, the molecule is Achiral. It is mathematically equivalent to a S2 axis of symmetry.
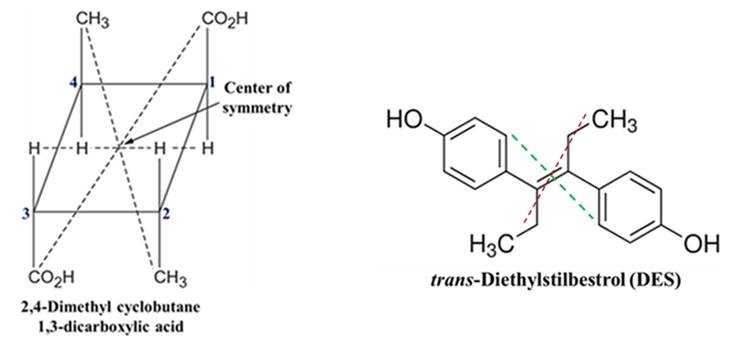
- Example: Look at certain cyclic drug intermediates trans-2,4-dimethylcyclobutane-1,3-dicarboxylic acid.
- Trans-Diethylstilbestrol (DES): DES is a synthetic nonsteroidal estrogen. The trans-isomer is a classic example used in medicinal chemistry to discuss structure-activity relationships. If you look at the center of the double bond (C=C), every group on one side (phenol ring, ethyl group) has an identical match diagonally opposite to it. As a result the inversion through the center makes this isomer achiral and optically inactive.
C. Proper Axis of Symmetry (Cn) – The “Rotational Spin”
This is all about rotation like a ceiling fan. If you can rotate a molecule by a certain angle and it looks exactly like the original, it has a proper Cn axis.
The Math: The formula is θ = 360°/n. Rotation by 360°/n gives identical structure. 180° rotation → it’s a C2 axis (360/180 = 2), 120° rotation → it’s a C3 axis (360/120 = 3) and so on. Having a Cn axis does not automatically make a molecule achiral.
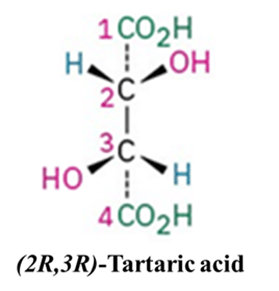
Example: (2R,3R)-Tartaric acid has a C2 axis. If you stick a pin through the center of the C2-C3 bond and rotate the molecule 180°, it looks exactly the same. Note that it has an axis but no plane. Therefore, it remains chiral and optically active.
D. Improper Axis of Symmetry (Sn)
This is the “advanced” element and the special move. It is also called “Rotation-Reflection Symmetry”. It’s a two-step dance:
- Rotation of the molecule by an angle (θ), where θ = 360°/n.
- Reflection through a plane perpendicular to the axis.
In the context of stereochemistry, n represents the order of the axis. It is a whole number that defines the degree of rotation performed during the symmetry operation. Crucial Point: If the resulting structure is identical to the original, the molecule has an Sn axis, it is achiral. This is the ultimate test for chirality.
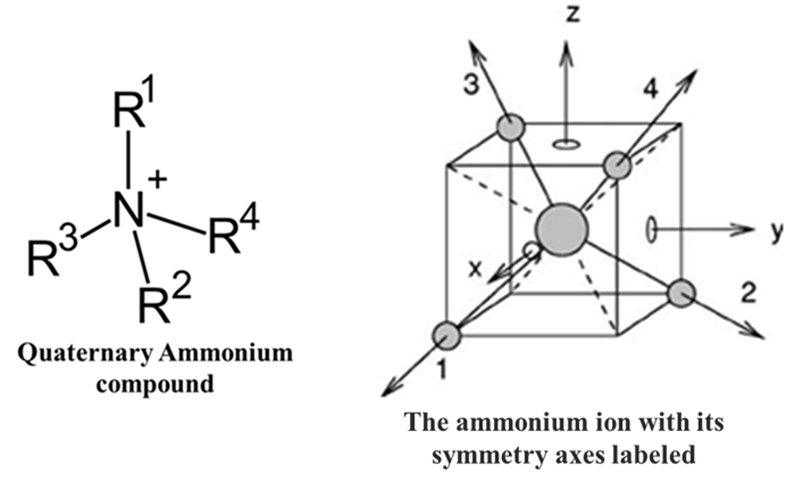
Example: While methane is a simple gas, its tetrahedral geometry is the foundation of all organic drug chemistry. Derivatives like Quaternary Ammonium compounds (used as neuromuscular blockers) often exhibit S4 symmetry. An S4 axis involves a 90° rotation followed by reflection. In a perfectly tetrahedral molecule like Methane or a symmetrical Ammonium salt (NR4+), this element exists.
Common Values of “n” and their Meanings:

Clinical Relevance
- Enzymes are Chiral: They distinguish between symmetric and asymmetric molecules.
- Optical Isomers: A drug with a plane of symmetry loses its handedness and therefore does not rotate plane-polarized light.
- Potency: One isomer might be a life-saving drug, while the symmetric version might be inactive or toxic.
Summary Table for Quick Revision
