Methods of expressing concentration

In analytical chemistry, concentration tells us exactly how much of a specific substance (the solute) is dissolved in a given amount of liquid (the solvent). Understanding these methods is the backbone of laboratory work, medicine, and industrial manufacturing. Here is a detailed guide to the most common methods of expressing concentration, explained in simple terms.

Molarity (M)

Molarity is the most widely used unit in chemistry labs. It defines the number of moles of solute per liter of solution.

Formula: M = moles of solute / liters of solution

Beyond just the basic formula, molarity is about the relationship between mass, volume, and the number of particles (moles). In a textbook, you are often given “moles.” In a lab, you are always given “grams.” This means every molarity problem usually starts with a conversion.

Mole (n): The number of particles (6.022 x10²³ particles per mole) i.e. Avogadro’s Number.
Molar Mass (MM): The weight of one mole of that substance (found on the periodic table).

Preparing a Solution

Molar solution is prepared in the Volumetric Flask. One of the most common mistakes is thinking that “1 Liter of solution” means adding 1 Liter of water to the powder. That is incorrect. If you add 1L of water to 100g of salt, the final volume will be more than 1L, which ruins your molarity. The correct method is as below:

Calculate and weigh the mass needed.
Add the solute to a volumetric flask.
Add some solvent (water) and swirl until the powder dissolves.
Fill to the mark: Add water drop-by-drop until the bottom of the meniscus touches the etched line on the volumetric flask neck.

Molarity Changes with Temperature

Molarity is temperature-dependent and based on Volume. Because liquids expand when heated and contract when cooled, the volume of final solution as well as molarity also changes slightly throughout the day.

Hot Day: Volume increases → Molarity decreases.
Cold Day: Volume decreases → Molarity increases.

This is why, for extremely precise research, scientists prefer Molality (m), which uses mass (Kg) because mass never changes, no matter the temperature.

Real-World Applications of Molarity

Molarity isn’t just for scientists in white coats; it is used to ensure safety and quality in everyday products.

Medicine: I.V. (Intravenous) drips must have a specific molarity of salts and glucose to match blood’s osmotic pressure. If the molarity is too high or too low, it can damage blood cells.
Soft Drinks: The “sweetness” of a soda is controlled by the molarity of sucrose. A typical soda has a sucrose molarity of about 0.375 M.
Agriculture: Fertilizers and pesticides are often sold as highly concentrated “stock” solutions that farmers must dilute to a specific molarity before spraying crops to avoid burning them.

The Problem and Solution

Prepare 250 mL of a 0.5 M (molar) solution of Sodium Hydroxide (NaOH). How many grams of solid NaOH do you need to weigh out?

Solution

Step 1: Identify the Molar Mass of NaOH

First, look at the periodic table to find the atomic weights:

Sodium (Na) ≈ 23.0 g/mol
Oxygen (O) ≈ 16.0 g/mol
Hydrogen (H) ≈ 1.0 g/mol
Total Molar Mass of NaOH = 23 + 16 + 1 = 40.0 g/mol

Step 2: Convert Volume to Liters

Molarity is always based on Liters. So, 250 mL= 0.25 Liters

Step 3: Find the moles

Rearrange the formula “M = moles\liters” to find the moles needed:

Moles = Molarity x Volume

Moles = 0.5 mol/L x 0.25 L = 0.125 moles

Step 4: Convert Moles to Grams

Now, multiply the moles by the molar mass:

Mass = 0.125 moles x 40.0 g/mol = 5.0 grams

Result: Weigh 5 grams of NaOH, place it in a volumetric flask, and add water until the total volume reaches the 250 mL mark.

Molality (m)

Molality (Molality (m) is the “gold standard” when accuracy is needed across different temperatures. It measures the concentration of a solution based on the mass of the solvent rather than the total volume of the solution. Molality is defined as the number of moles of solute per kilogram of solvent. Molality depends on mass. Since mass does not change when you heat or cool a liquid, the molality remains exactly the same whether you are in a freezing lab or a hot factory.

Formula: m = moles of solute/ mass of solvent in kilograms
Key Fact: Since mass does not change with temperature, molality is more precise for thermodynamic calculations.

Example: If you add 0.5 moles of sugar to 1 kg of water, the concentration is 0.5 m (molal).

Practical Uses:

Molality is the primary unit used when studying Colligative Properties. This is the physical characteristics of solutions that depend only on the number of solute particles dissolved. It involve boiling/freezing points, vapor pressure, osmotic pressure. These are physical changes that happen to a liquid when you add a solute, such as:

Freezing Point Depression: Why we put salt on icy roads (it lowers the freezing point of water).
Boiling Point Elevation: Why salt water takes longer to reach a boil than pure water.
Antifreeze: Ensuring car radiators don’t freeze in winter or overheat in summer.

The Problem and solution

Dissolve 20 grams of Glucose (C₆H₁₂O₆) into 500 grams of water. What is the molality?

Solution

Step 1: Find the moles of solute

Molar mass of Glucose = 180 g/mol
Moles = 20g / 180g/mol = 0.111 moles

Step 2: Convert solvent mass to Kilograms

The solvent is water.
500 g = 0.5 kg

Step 3: Solve for Molality

m = 0.111 moles/ 0.5 kg = 0.222 m

Comparison: Molarity vs. Molality

Feature	Molarity (M)	Molality (m)
Denominator	Liters of Solution	Kilograms of Solvent
Temperature	Changes with temperature	Constant at all temperatures
Primary Use	Titrations & general lab work	Thermodynamics & Colligative properties
Ease of Prep	Needs a Volumetric Flask	Needs a Digital Balance

How to convert between Molarity and Molality?

It is a favorite topic for chemistry to convert between Molarity (M) and Molality (m) because it requires to understand the difference between the mass of the solvent and the volume of the entire solution. To do this, the density of the solution must be known.

Example: You have a 3.0 M solution of Sodium Chloride (NaCl). The density of this solution is 1.12 g/ml. What is the Molality?

Step 1: Find Mass of solute (NaCl)

To make the math simple, let’s assume we have 1 Liter (1000 mL) of solution.

From the Molarity (3.0 M), we know we have 3.0 moles of NaCl.
Molar mass of NaCl = Na (23) + Cl (35.5) = 58.5 g/mol
Mass of solute (NaCl): 3.0 moles x 58.5 g/mol = 175.5 g.

Step 2: Find the Total Mass of the Solution

Use the density to see how much that 1 Liter actually weighs on a scale.

Total Mass = Volume x Density
Total Mass = 1000 mL x 1.12 g/mL = 1120 g.

Step 3: Find the Mass of the Solvent (Water)

This is the “trick” step. Remember: Total Mass = Solute Mass + Solvent Mass.

Solvent Mass = Total Mass – Solute Mass
Solvent Mass = 1120 g – 175.5 g = 944.5 g.
Convert to kg: 0.9445 kg.

Step 4: Calculate Molality

Now, use the molality formula:

m = moles of solute/kg of solvent

m = 3.0 moles / 0.9445 kg = 3.176 m

Note: In dilute aqueous solutions, Molarity and Molality are very close. But as the solution gets concentrated, the values start to drift apart.

Normality (N)

Normality is often used in acid-base titrations. It measures the gram equivalent weight of a solute per liter of solution. It basically looks at the “reactive capacity” of a chemical. It is specifically used in reactions where one molecule can provide multiple reactive parts (like H⁺ ions in acids or OH^– ions in bases).

Formula: N = Gram equivalents of solute / Volume of solution in Liters

Here are the two easiest ways to calculate it.

Method 1: From Molarity

It is done for solution through the formula N = M x n

where M is molarity (moles per liter) & n is the number of reactive units, like H⁺ ions in an acid and OH^– ions in bases.

Finding the n-factor (n)

Substance	Replaceable H⁺/ OH^–	n-factor
HCl	1 replaceable H⁺	n=1
H₂SO₄	2 replaceable H⁺	n=2
NaOH	1 replaceable OH^–	n=1
Ca(OH)₂	2 replaceable OH^–	n=2
H₃PO₄	3 replaceable H⁺	n=3

Example: What is the Normality of a 2 M solution of Sulfuric Acid (H₂SO₄)?

Since H₂SO₄has 2 hydrogen ions to donate, n = 2. So, N = 2M x 2 = 4 N

Method 2: From Grams

Step A: Find the Equivalent Weight = Molar Mass/n-factor

Step B: Find the Gram Equivalents = Mass of Solute (grams)/Equivalent Weight

Step C: Calculate Normality (N) = Gram Equivalents/Volume of solution (Liters)

Mass (g)= Normality x Equivalent Weight x Volume (L)

Normality = Mass (g)/ Equivalent Weight x Volume (L)

Example: Prepare a 1 Liter 1N Sodium Hydroxide (NaOH) solution.

NaOH provides exactly one hydroxide ion (OH^–) per molecule, its Normality is equal to its Molarity.

Molar Mass of NaOH: 23 (Na) + 16 (O) + 1 (H) = 40 g/mol.

Equivalent Weight: Since NaOH has one reactive OH^– group, its equivalent weight is =40 / 1 = 40 g/eq.

For 1 Liter: 1 N x 40 g/eq x1 L = 40 grams.

Result: Weigh 40 grams of NaOH, place it in a volumetric flask, and add water until the total volume reaches the 1000 mL mark.

Mass Percentage (% w/w)

This is a simple way to express concentration by comparing the mass of the solute to the total mass of the solution. It is commonly used in industrial chemicals and household products (like bleach).

Formula: Mass % = (mass of solute/total mass of solution) x 100

Example: A “5%w/w NaCl solution ” means there are 5g of salt in 100g of the total solution.

Convert Molarity to Mass Percentage

The Challenge: You have a 2.0 M solution of Sodium Chloride (NaCl). The density of the solution is 1.08 g/mL. What is the Mass Percentage (% w/w) of NaCl in this solution?

Step 1: Assume a Volume to have 1 Liter (1000 mL) of the solution

Step 2: Find the Mass of the Solute: From the molarity (2.0 M), we know there are 2.0 moles of NaCl in that 1 Liter.

Molar Mass of NaCl: 23.0 + 35.5 = 58.5 g/mol
Mass of Solute: 2.0 moles x 58.5 g/mol = 117 g

Step 3: Find the Total Mass of the Solution: Use the density to convert 1000 mL volume into mass:

Mass = Density x Volume
Total Mass = 1.08 g/mL x 1000 mL = 1080 g

Step 4: Calculate Mass Percentage: Now, apply the formula:

Mass % = (mass of solute/ total mass of solution) x 100

Mass% = (117 g/ 1080 g) x 100 = 10.83%

Parts Per Million (ppm) and Parts Per Billion (ppb)

In analytical chemistry, ppm and ppb are units used to express extremely low concentrations of a substance—often called “trace” concentrations. These are most commonly used in environmental science to measure pollutants in water or air.

What is Parts Per Million (ppm)?

Think of ppm as a ratio. It represents one unit of solute in one million (10 lakhs) units of the total solution. Its common use is to determine Fluoride in water, CO₂ in air etc.

Mathematically: ppm = 1 part of solute/10⁶ parts of solution
In terms of Mass: For solids or liquids, 1ppm is equivalent to 1 milligram (mg) of solute in 1 kilogram (kg) of solution.
In Water: Since 1 Kg of water weighs 1 L, 1 ppm = 1 mg/L

What is Parts Per Billion (ppb)?

ppb is used when a substance is so toxic or rare that even “parts per million” is too large a unit. It represents one unit of solute in one billion (100 Crore) units of solution. It is applied in determination of pesticides, heavy metals (Lead) etc.

Mathematically: ppb = 1 part of solute/10⁹ parts of solution
In terms of Mass: 1ppb is equivalent to 1 microgram (μg) of solute in 1 kilogram (kg) of solution.
In Water: 1 ppb = 1 μg/L

Calculate ppm and ppb

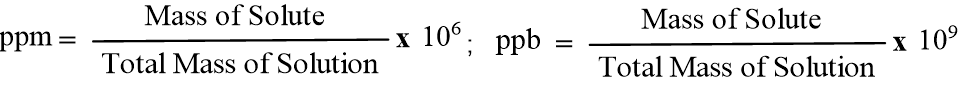
Example Calculation: If a 2 kg sample of soil contains 0.004 grams of arsenic, what is the concentration in ppm?

Convert grams to milligrams: 0.004 g = 4 mg
Divide by kg: 4 mg/ 2 kg = 2 ppm

Mole Fraction (χ)

The mole fraction represents the ratio of the moles of one component to the total moles of all components in the mixture. It has no units. It is generally presented by lowercase Greek letter chi (χ) or the lowercase Roman letter x.

Formula: χ _A = moles of A/ total moles in mixture

Example: In a mixture of 2 moles of Alcohol and 8 moles of Water, the mole fraction of Alcohol is 2 / 10 = 0.2.

Summary Comparison Table

Method	Symbol	Basis	Best Use Case
Molarity	M	Vol. of Solution	Daily Lab Work
Molality	m	Mass of Solvent	Temp-sensitive experiments
Normality	N	Equivalents	Titrations
Mass %	%	Total Mass	Commercial Products
ppm / ppb	ppm	Mass Ratio	Environmental Testing